RESUMEN DE LO VISTO EN LAS DESIGUALDADES

Es la desigualdad existente entre dos expresiones algebraicas, conectadas a través de los signos: mayor que >, menor que <, menor o igual que ≤, así como mayor o igual que ≥, en la que figuran uno o varios valores desconocidos llamadas incógnitas, además de ciertos datos conocidos.

La desigualdad existente entre las dos expresiones algebraicas sólo se verifica, o más bien, solo es verdadera para determinados valores de la incógnita.

La solución de una inecuación formulada, significa determinar mediante ciertos procedimientos, el valor que la satisfaga. 

Clasificación de las inecuaciones

Existen diferentes tipos de inecuaciones. Estas, se pueden clasificar de acuerdo al número de incógnitas y de acuerdo al grado de ellas. Para saber el grado de una inecuación, basta con identificar el mayor ellos. Así, tenemos los tipos siguientes:


De una incógnita
De dos incógnitas
De tres incógnitas
De n incógnitas
De primer grado
De segundo grado
De tercer grado
De cuarto grado
Inecuaciones de grado N

(GRACIAS POR SU PARTICIPACION)

SISTEMA DE DESIGUALDADES LINEALES CON DOS VARIABLES

 Sistema de desigualdades lineales con dos variables 

El conjunto solución de un sistema de desigualdades es la intersección de las regiones  solución de cada desigualdad.

EJEMPLOS:

1. Representa gráficamente el conjunto solución del sistema y > 2 , x ≤ -1

Solución: 

Se encuentra la  región solución de cada desigualdad. La solución es el conjunto de todos los puntos que se encuentren en la intersección de las regiones.

2. Determina gráficamente el conjunto solución del sistema y ≥ x-2, x + y -1< 0

Solución:  

En sistema tiene la forma 

y ≥ x-2

y < 1-x

Se grafica la recta y = x-2, con la líneal continua ya que el signo de la desigualdad indica intervalo cerrado; luego, se grafica la recta y = 1-x, con una línea punteada, ya que el signo de la desigualdad indica intervalo abierto. Se grafica la región solución de cada desigualdad y la intersección de las regiones son todos los puntos que satisfacen el conjunto solución del sistema.

Finalmente, la grafica que representa a la región que contiene el conjunto de todos los pares ordenados es: 

GRAFICA DE UNA DESIGULADAD LINEAL CON DOS VARIABLES

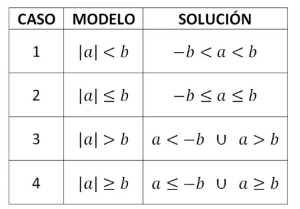
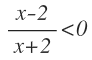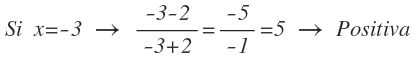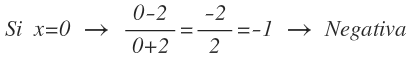 Gráfica de una desigualdad lineal con dos variables 

    Una desigualdad lineal que tiene la forma: 

a) y < mx + b no incluye a la recta.   c) y > mx + b no incluye a la recta 

b) y ≤ mx + b incluye a la recta.       a) y ≥ mx + b incluye a la recta 

En una desigualdad lineal de dos variables, el conjunto solución es la región que se forma por el conjunto de todos los pares ordenados ( x, y) que satisfacen la desigualdad.

EJEMPLOS 

1. Determina la grafica del conjunto solución de y > -2 

Solución : 

Primero se grafica la recta y = -2, con una línea punteada, ya que el signo de la desigualdad representa un intervalo abierto.

Luego se  sombrea la  región que contiene a todos los puntos de ordenada estrictamente mayores que -2, en este caso son todos los puntos que se encuentran por arriba de la recta punteada.

2. Encuentra la  región del conjunto solución de x ≤ 5.

Solución:

Se grafica la recta x = 5, el signo de la desigualdad indica que la  es línea continua.

El conjunto solución son los puntos del plano cuyas abscisas son menores o iguales a 5.

3. Determina la grafica del conjunto solución de y > x + 2 .

Solución: 

Se grafica y = x + 2; esta se representa con una recta punteada, ya que el signo representa intervalo abierto, la recta divide al plano cartesiano en 2 planos.

Para determinar la región solución del sistema, se sustituye en un punto perteneciente a una de las regiones y se verifica que cumpla con la desigualdad. Por ejemplo, el punto ( -1, 4) 

y > x + 2 

4 > -1+2

4 > 1

El punto satisface la desigualdad.

La región que es la solución de la desigualdad, es el conjunto de puntos que están en la región  por arriba de la recta punteada, es decir, el conjunto de puntos que se encuentran en el plano I.

Por el contrario, si el punto elegido no satisface la desigualdad, la que región presenta el conjunto solución será el plano contrario al punto. 

DESIGUALDADES CON VALOR ABSOLUTO

 Desigualdades con valor absoluto 

El conjunto solución de una desigualdad que involucra valor absoluto, está dado por las siguientes propiedades : 

Sean a, b ϵ R y b > 0

1. | a | < b se expresa como:                                   

-b < a < b o bien a > -b y a < b

2.  | a | ≤ b se expresa como: 

-b ≤ a ≤ b o bien a ≥ -b y a ≤ b 

3.  | a | > b se expresa como: 

-a > b o a > b o bien  a < -b o a > b

4. | a | ≥ b se expresa : 

-a ≥ b o a ≥ b o bien a ≤ -b o a ≥ b

EJEMPLOS

1. Determina el conjunto solución de | x+1| < 7.

SOLUCION

La desigualdad  | x+1| < 7, tiene tiene la forma de la propiedad 1, entonces :  -7 <  x+1 < 7   

o bien:     

 -7 <  x+1                            

-7-1 <  x

-8 <  x

x+1 < 7

x < 7-1

x < 6  

Por lo consiguiente, el conjunto solución es el intervalo (-8,6)

2. Encuentra el conjunto solución de  | 2x-1|  ≥ 7

SOLUCION 

La desigualdad | 2x-1|  ≥ 7 tiene la forma de la propiedad 4, entonces: 

-( 2x-1)  ≥ 7

-2x+1 ≥ 7

-2x ≥ 7-1

-2x ≥ 6

x ≤ -6/2

x ≤ -3

2x-1 ≥ 7

2x ≥ 7+1

2x ≥ 8

x ≥ 8/2

x ≥ 4 

Por consiguiente, el conjunto solución es: (-∞, -3] ∪ [ 4, ∞)

DESIGUALDAD QUE TIENE LA EXPRESION (x-a) (x-b) (x-c)...

 Desigualdad que tiene la expresión (x-a) (x-b) (x-c)...👀

Una forma practica para determinar el conjunto solución, es construir una tabla con los intervalos que se forman al encontrar los valores que hacen cero a cada factor, como se ilustra en el siguiente ejemplo.

🌟Ejemplo:

Resuelve la desigualdad (x-2)(x-4)(x+2) ≥ 0

🌟Solución:

Se determinan los valores que hacen cero a cada factor para formar los intervalos.

Para x-2 =  0 ---- x = 2  ; Para x-4 = 0 ---- x = 4  ;  Para x+2 = 0 ----x = -2

La desigualdad indica que el producto es positivo, entonces se toman los intervalos cuyo producto es positivo, es decir [ -2,2] y [ 4,∞), luego la unión de estos intervalos es el conjunto solución.

Finalmente, la solución de la desigualdad es : [ -2,2] ∪ [ 4,∞) 

🌟Practiquemos lo aprendido siguiendo los pasos del ejemplo anterior.

🌟Determinar  el conjunto solución de la siguiente desigualdad :

1. (x+2) (x-4) ( 2-x) (x+1) ≥  0 

Finalmente, la solución de la desigualdad  es : [ -2,-1] ∪ [ 2,4]

¡PROXIMO TEMA  A ESTUDIAR DESIGUALDADES CON VALOR ABSOLUTO!

 

 Inecuaciones racionales o fraccionarias

Resolver una inecuación racional consiste en obtener el rango de valores de x cumplan la desigualdad, es decir, obtener los tramos para los que la función sea positiva o negativa, según sea la desigualdad de la inecuación.

1. Obtener antes los valores de x donde la función cambia de signo, de positiva a negativa o viceversa
2. Representar los puntos en la recta real, teniendo en cuenta si se coge o no para el resultado.
3. Calcular el signo de cada intervalo.
4. El rango o los rangos de valores que cumplan la desigualdad, será la solución de la inecuación.

Inecuaciones resueltas paso a paso

Vamos a resolver ahora unas cuantas inecuaciones racionales paso a paso, aplicando el procedimiento que acabamos de ver.

Ejemplo resuelto de inecuación racional 1

En esta inecuación debemos calcular los intervalos donde la función racional es menor que cero, es decir, los intervalos donde la función racional sea negativa.

Para ello vamos a obtener en primer lugar los puntos donde la función cambia de signo.

Esos puntos los obtenemos igualando el numerador a cero por un lado e igualando el denominador a cero por otro lado.

Igualamos el numerador a cero:

Y despejamos x:

Por otro lado, igualamos el denominador a cero:

Y despejamos la x:

Representamos ambos valores que acabamos de obtener en la recta real:

El valor que resulta de igualar el numerador a cero, se coge siempre y cuando la desigualdad tenga un signo igual. En nuestro caso, el 2 no se coge, ya que la desigualdad no tiene signo igual, por lo que dejamos el punto hueco.

Por otro lado, el valor que resulta de igualar el denominador a cero, nunca se coge, ya que el denominador de una función racional nunca puede ser cero. Por tanto, el -2, también queda hueco.

Ahora vamos a obtener el signo de cada intervalo.

Para esto, debemos darle a x un valor que pertenezca a cada tramo.

Para saber el signo del tramo que queda a la izquierda de -2, le damos a x el valor de -3 en la función y operamos:

El resultado es 5, mayor que cero, luego cualquier valor de x que esté en ese tramo hará que la función sea positiva, por lo que la función es positiva en ese intervalo.

Para le tramo que está entre -2 y 2 la damos a x el valor de 0, sustituimos en la en la función y operamos:

El resultado es -1, menor que cero. Cualquier valor de x que pertenezca a este tramo hará que la función sea negativa, por lo que la función es negativa en ese tramo.

Finalmente, para el tramo que queda a la derecha del 2, le damos a x el valor de 3, lo sustituimos en la función y operamos:

El valor de la función es mayor que cero, por lo que la función será positiva en ese tramo.

Representamos el signo de cada tramo en el recta real:

Para terminar, la solución de nuestra inecuación son los valores de x que hacen que la función sea menor que cero, es decir los tramos negativos:

Por tanto la solución es el intervalo abierto desde -2 hasta 2 (ambos sin cogerlo por las razones que he comentado más arriba):

ILUSTRACION

DESIGUALDAD CUADRATICA CON UNA

Desigualdad cuadrática 

Este suplemento tiene el propósito de mostrar como resolver desigualdades que contienen una expresión cuadrática o una expresión racional. Los métodos que presentaremos difieren de los desarrollados para resolver desigualdades lineales. Como parte del proceso de resolver la desigualdad cuadrática la rearreglaremos para que un lado sea igual a cero. Luego factorizaremos la expresión cuadrática que se obtiene.

Ejemplo 1. Resuelva la desigualdad x² + x − 2 > 0.

SOLUCION:  Comenzamos factorizando la expresión cuadrática pues uno de los lados es igual a cero.

                      x² + x − 2 > 0             (x + 2)(x − 1) > 0

 Ahora resolvemos la ecuación (x + 2)(x − 1) = 0. 

               Tenemos que x + 2 = 0 o x − 1 = 0.

Obtenemos que x = −2 o x = 1. Estos valores dividen la recta real en tres intervalos: (−∞,−2), (−2,1), (1,∞). Sabemos que x = −2 y en x = 1 satisfacen la ecuación x² + x − 2 = 0. Deseamos determinar el signo de la expresión x² + x − 2 en los intervalos (−∞,−2), (−2,1), (1,∞). Para esto determinamos el signo de cada uno de los factores usando un valor de x en cada uno de los intervalos. Este valor particular de x se conoce como valor prueba. Por ejemplo, para determinar el signo del factor x − 2 en el intervalo (−∞,−2) escogemos un valor de x que este en este intervalo, digamos x = −3 y lo subustituimos en x − 2. Obtenemos x − 2 = −3 − 2 = −5. Luego x − 2 es negativo en el intervalo (−∞,−2). Por otro lado x−1 = −3−1 = −4 por lo que x−1 es negativo en el intervalo (−∞,−2). Repetimos este procedimiento para los otros dos intervalos. Construimos una tabla, llamada una tabla de signos, para organizar la información obtenida:

📔

📔

Intervalos	(−∞,−2)	(−2,1)	(1,∞)
Signo de x + 2	−	+	+
Signo de x − 1	−	−	+
Signo de (x + 2)(x − 1)	+	−	+

l signo de (x + 2)(x − 1) se obtiene multiplicando el signo de x − 2 con el signo de x + 1. Nos interesa saber donde (x + 2)(x − 1) > 0, es decir donde (x + 2)(x − 1) es positiva. Esto ocurre en (−∞,−2) o en (1,∞).

Ejemplo 2. Resuelva la desigualdad x² ≤ 4x + 12.

SOLUCION: Primero despejemos para que un lado de la desigualdad sea cero y factoricemos la expresión  resultantes

                                x² ≤ 4x + 12          x² − 4x − 12 ≤ 0                 (x + 2)(x − 6) ≤ 0.

Resolvemos la ecuación (x + 2)(x − 6) = 0. Obtenemos que x + 2 = 0 o x − 6 = 0. Luego x = −2 o x = 6. Ahora construimos una tabla de signos.

📔
📔

Intervalos	(−∞,−2)	(−2,6)	(6,∞)
Signo de x + 2	−	+	+
Signo de x − 6	−	−	+
Signo de (x + 2)(x − 6)	+	−	+

Buscamos los valores x tales que (x + 2)(x − 6) ≤ 0. (x + 2)(x − 6) es menor que cero en el intervalo (−2,6) e igual a cero en x = −2 y en x = 6. Luego la solución de la desigualdad es el intervalo [−2,6].