Inecuaciones racionales o fraccionarias
Resolver una inecuación racional consiste en obtener el rango de valores de x cumplan la desigualdad, es decir, obtener los tramos para los que la función sea positiva o negativa, según sea la desigualdad de la inecuación.
- Obtener antes los valores de x donde la función cambia de signo, de positiva a negativa o viceversa
- Representar los puntos en la recta real, teniendo en cuenta si se coge o no para el resultado.
- Calcular el signo de cada intervalo.
- El rango o los rangos de valores que cumplan la desigualdad, será la solución de la inecuación.
Inecuaciones resueltas paso a paso
Vamos a resolver ahora unas cuantas inecuaciones racionales paso a paso, aplicando el procedimiento que acabamos de ver.
Ejemplo resuelto de inecuación racional 1
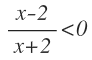
En esta inecuación debemos calcular los intervalos donde la función racional es menor que cero, es decir, los intervalos donde la función racional sea negativa.
Para ello vamos a obtener en primer lugar los puntos donde la función cambia de signo.
Esos puntos los obtenemos igualando el numerador a cero por un lado e igualando el denominador a cero por otro lado.
Igualamos el numerador a cero:
![]()
Y despejamos x:
![]()
Por otro lado, igualamos el denominador a cero:
![]()
Y despejamos la x:
![]()
Representamos ambos valores que acabamos de obtener en la recta real:

El valor que resulta de igualar el numerador a cero, se coge siempre y cuando la desigualdad tenga un signo igual. En nuestro caso, el 2 no se coge, ya que la desigualdad no tiene signo igual, por lo que dejamos el punto hueco.
Por otro lado, el valor que resulta de igualar el denominador a cero, nunca se coge, ya que el denominador de una función racional nunca puede ser cero. Por tanto, el -2, también queda hueco.
Ahora vamos a obtener el signo de cada intervalo.
Para esto, debemos darle a x un valor que pertenezca a cada tramo.
Para saber el signo del tramo que queda a la izquierda de -2, le damos a x el valor de -3 en la función y operamos:
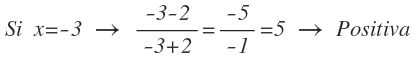
El resultado es 5, mayor que cero, luego cualquier valor de x que esté en ese tramo hará que la función sea positiva, por lo que la función es positiva en ese intervalo.
Para le tramo que está entre -2 y 2 la damos a x el valor de 0, sustituimos en la en la función y operamos:
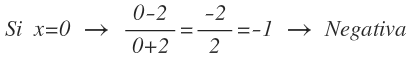
El resultado es -1, menor que cero. Cualquier valor de x que pertenezca a este tramo hará que la función sea negativa, por lo que la función es negativa en ese tramo.
Finalmente, para el tramo que queda a la derecha del 2, le damos a x el valor de 3, lo sustituimos en la función y operamos:
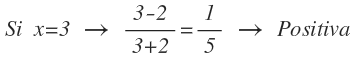
El valor de la función es mayor que cero, por lo que la función será positiva en ese tramo.
Representamos el signo de cada tramo en el recta real:
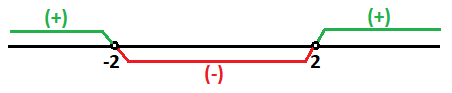
Para terminar, la solución de nuestra inecuación son los valores de x que hacen que la función sea menor que cero, es decir los tramos negativos:
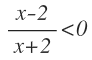
Por tanto la solución es el intervalo abierto desde -2 hasta 2 (ambos sin cogerlo por las razones que he comentado más arriba):
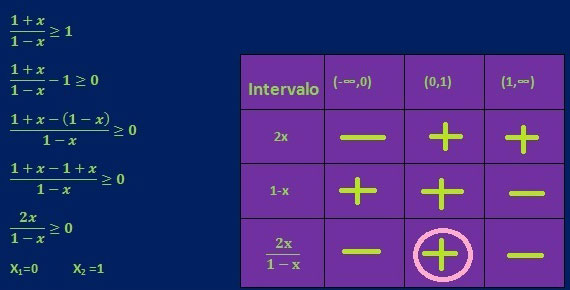

Excelente informacion
ResponderEliminarExcelente trabajo👍
ResponderEliminarMuy buena información.
ResponderEliminarMe parece muy buen contenido.
ResponderEliminar