DESIGUALDADES CON VALOR ABSOLUTO

 Desigualdades con valor absoluto 

El conjunto solución de una desigualdad que involucra valor absoluto, está dado por las siguientes propiedades : 

Sean a, b ϵ R y b > 0

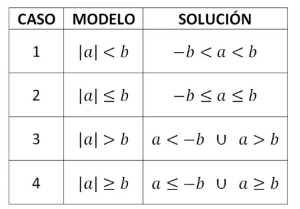
1. | a | < b se expresa como:                                   

-b < a < b o bien a > -b y a < b

2.  | a | ≤ b se expresa como: 

-b ≤ a ≤ b o bien a ≥ -b y a ≤ b 

3.  | a | > b se expresa como: 

-a > b o a > b o bien  a < -b o a > b

4. | a | ≥ b se expresa : 

-a ≥ b o a ≥ b o bien a ≤ -b o a ≥ b

EJEMPLOS

1. Determina el conjunto solución de | x+1| < 7.

SOLUCION

La desigualdad  | x+1| < 7, tiene tiene la forma de la propiedad 1, entonces :  -7 <  x+1 < 7   

o bien:     

 -7 <  x+1                            

-7-1 <  x

-8 <  x

x+1 < 7

x < 7-1

x < 6  

Por lo consiguiente, el conjunto solución es el intervalo (-8,6)

2. Encuentra el conjunto solución de  | 2x-1|  ≥ 7

SOLUCION 

La desigualdad | 2x-1|  ≥ 7 tiene la forma de la propiedad 4, entonces: 

-( 2x-1)  ≥ 7

-2x+1 ≥ 7

-2x ≥ 7-1

-2x ≥ 6

x ≤ -6/2

x ≤ -3

2x-1 ≥ 7

2x ≥ 7+1

2x ≥ 8

x ≥ 8/2

x ≥ 4 

Por consiguiente, el conjunto solución es: (-∞, -3] ∪ [ 4, ∞)